Jednostavni RLC-spojevi

Serijski RL-spoj

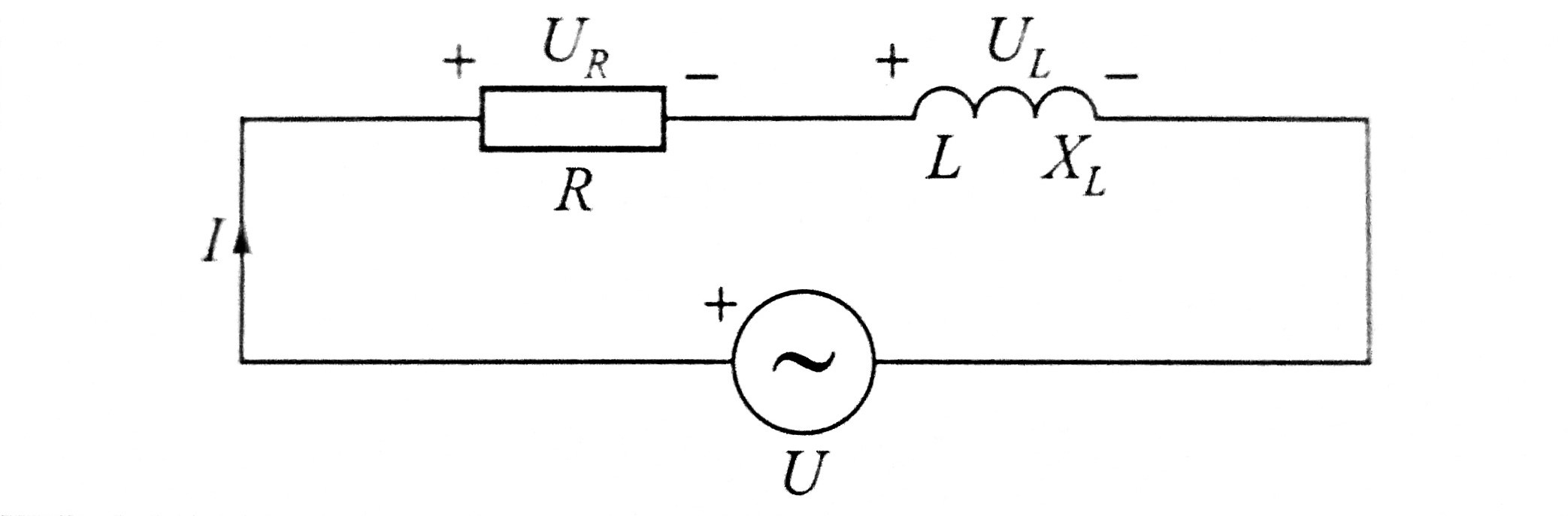
Na slici serijski spoj otpora i induktiviteta (s oznakama efektivnih vrijednosti struje i napona). Kod serijskog spoja otpora struja je zajednička, a ukupni napon je zbroj napona na otporima.

Kod serijskog spoja raznih vrsta otpora (ovdje su to radni otpor R i induktivni otpor X_L), naponi su međusobno pomaknuti u fazi, pa se ne može jednostavno zbrojiti njihove efektivne vrijednosti, nego treba uzeti u obzir i njihov fazni pomak. U tu svrhu se crta vektorski prikaz napona (vektorski dijagram), i naponi se zbrajaju vektorski.

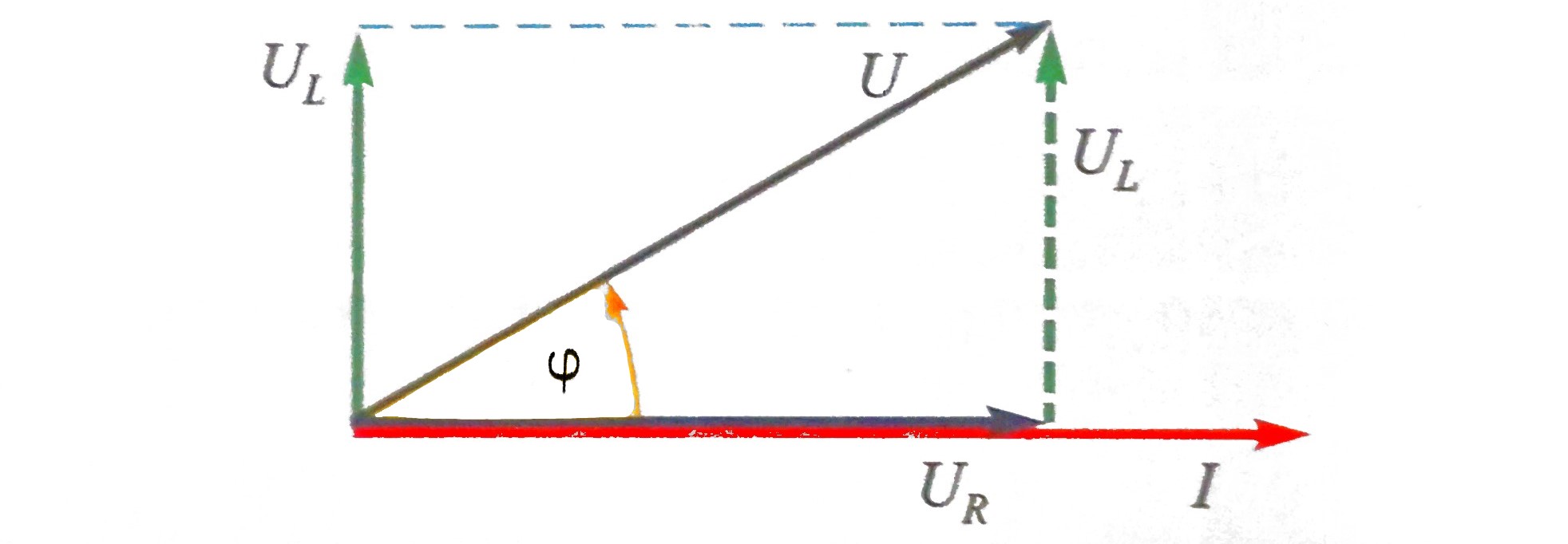
Vektorski dijagram započinjemo crtati sa zajedničkom veličinom, a to je u serijskom spoju struja. Vektor struje I uzima se s početnim kutem 0, pa se prema njemu postavljaju vektori napona na induktivitetu U_L i napon na otporu U_R (slika).

Napon na otporu U_R u fazi je sa strujom I, dok napon na induktivitetu U_L prethodi struji za 90°.

Vektor napona izvora U jednak je vektorskom zbroju napona na otporu U_R i induktivitetu U_L.

Ova tri napona čine pravokutni trokut pa vrijedi: $$ U^2= U^2_R + U^2_L $$ Kut napona U prema struji je pozitivan, tj. ukupni napon prethodi struji za neki kut $ \; φ \; \; (0° \lt φ \lt 90°) $.

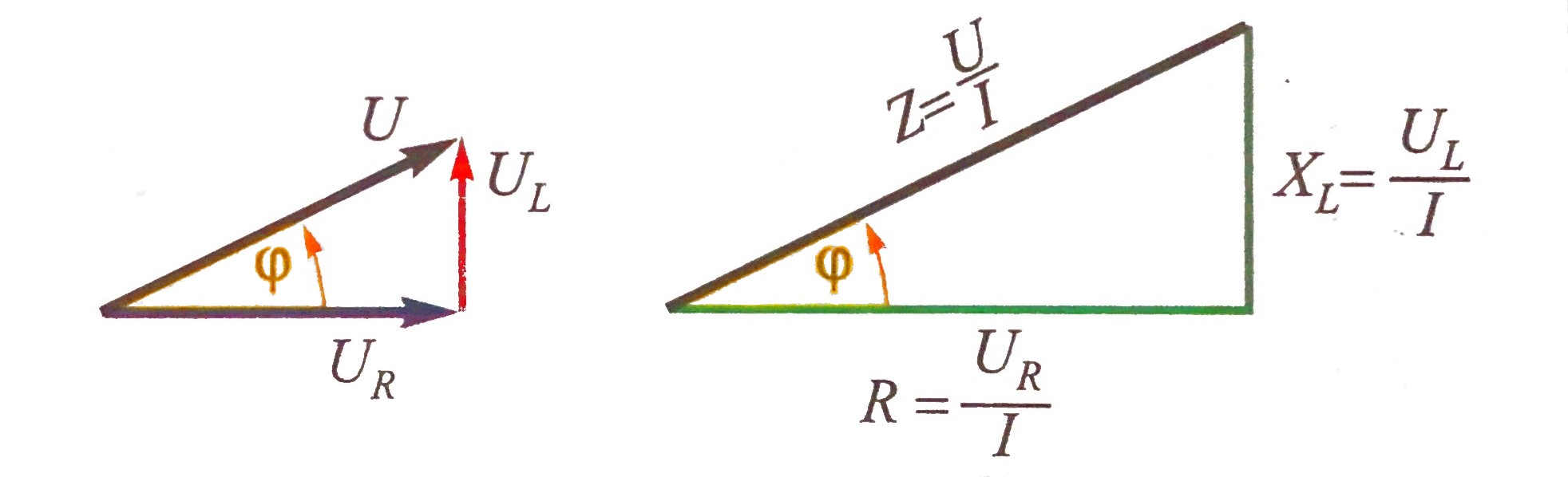
Dijeljenjem svake stranice trokuta napona s I, dobiva se sličan pravokutni trokut s katetama jednakim radnom otporu R i induktivnom otporu X_L (slika). On se naziva tokut otpora.

Hipotenuza ovog trokuta jednaka je omjeru ukupnog napona U i struje I spoja. Taj omjer ne predstavlja nikakav stvarni otpor, pa se naziva prividni otpor (ili impendancija) i označava sa Z. $$ Z^2= R^2 + X^2_L $$ Kut φ (između R i Z) naziva se i kut impendancije.

Pomnože li se stranice trokuta napona sa strujom I, dobiva se sličan pravokutni trokut u kojemu se katete jednake radnoj snazi P i jalovoj snazi Q_L. Taj trokut naziva se trokut snage (slika).

Hipotenuza trokuta snage jednaka je umnošku ukupnog napona U i struje I spoja. Umnožak $UI$ ne predstavlja snagu ni na jednom elementu kruga, pa se naziva prividna snaga i označava se sa S. Prividna snaga izražava se u voltamperima (VA).

Trokut daje odnos prividne, radne i jalove snage $$ S^2= P^2 + Q^2_L $$ Omjer radne snage P i prividne snage S naziva se faktor snage spoja (još se označava i kao $ \cos φ $)

Serijski RC-spoj

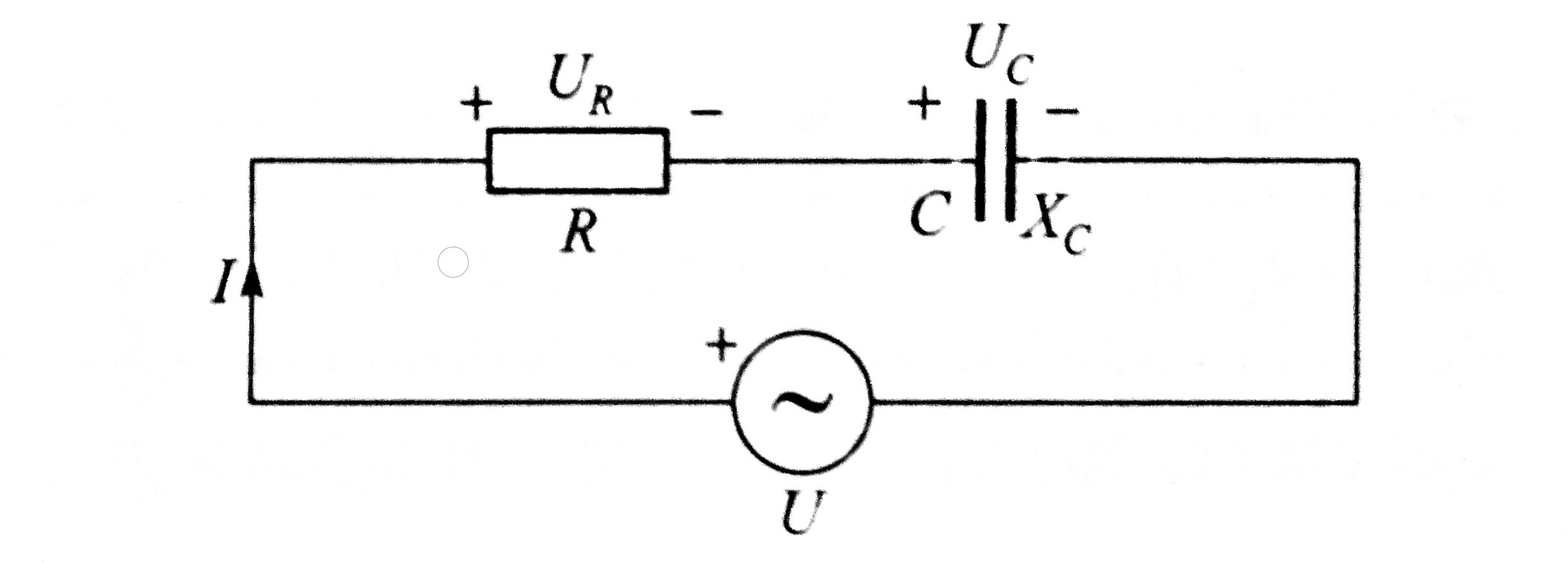
Slika prikazuje serijski spoj otpora R i kapaciteta C, kroz koje izvor napona U tjera struju I.

U vektorskom dijagramu (slika) vektor struje I uzimamo referentnim (s početnim kutem nula). Napon na otporu U_R u fazi je sa strujom, a napon na kapacitetu U_C zaostaje u fazi iza struje za 90°.

Vektorski zbroj napona na otporu U_R i napona na kapacitetu U_C daje napon izvora U. Ovi naponi čine pravokutni trokut iz kojeg proizlazi da je $$ U^2= U^2_R + U^2_L $$ Ovdje je kut napona U prema struji negativan, tj. napon U zaostaje iza struje za kut $ \; φ \; \; (-90° \lt φ \lt 0°) $.

U trokut otpora, dobivenom iz trokuta napona (slika), zbog negativnog kuta φ kapacitivni otpor X_C je ispod radnog otpora R (nasuprot induktivnog otpora X_L u trokutu otpora RL-kruga).

Prividni, radi i reaktivni (kapacitivni) otpor povezani su i ovdje Pitagorinim poučkom $$ Z^2= R^2 + X^2_C $$ U trokutu snage (slika), zbog negativnog kuta φ kapacitivna jalova snaga Q_C je ispod radne snage P, suprotno od induktivne snage Q_L u trokutu snage RL-kruga.

Prividna, radna i jalova (kapacitivna) snaga povezane su također putem Pitagorina poučka $$ S^2= P^2 + Q^2_C $$ Faktor snage i ovdje se, kao i u bilo kojem spoju, računa se kao omjer radne i prividne snage $ (P/S) $.

Serijski RLC-spoj

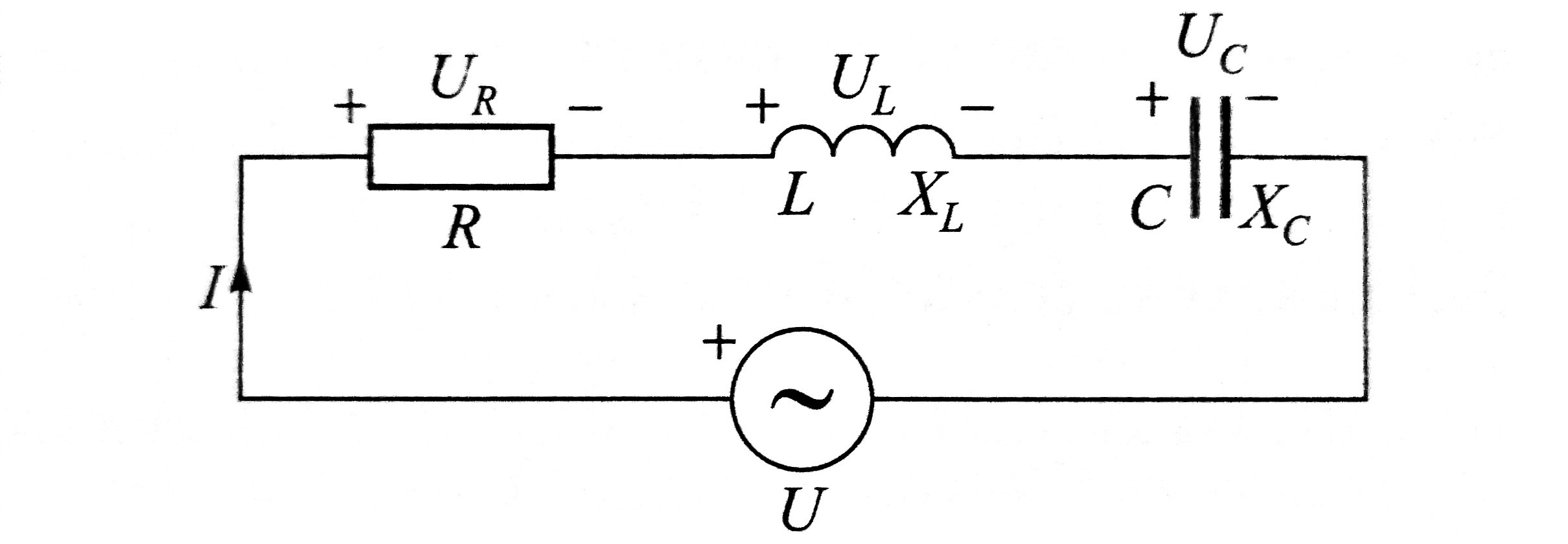
U serijskom RLC-krugu (slika) uz radni otpor R su induktivni otpor X_L i kapacitivni otpor X_C.

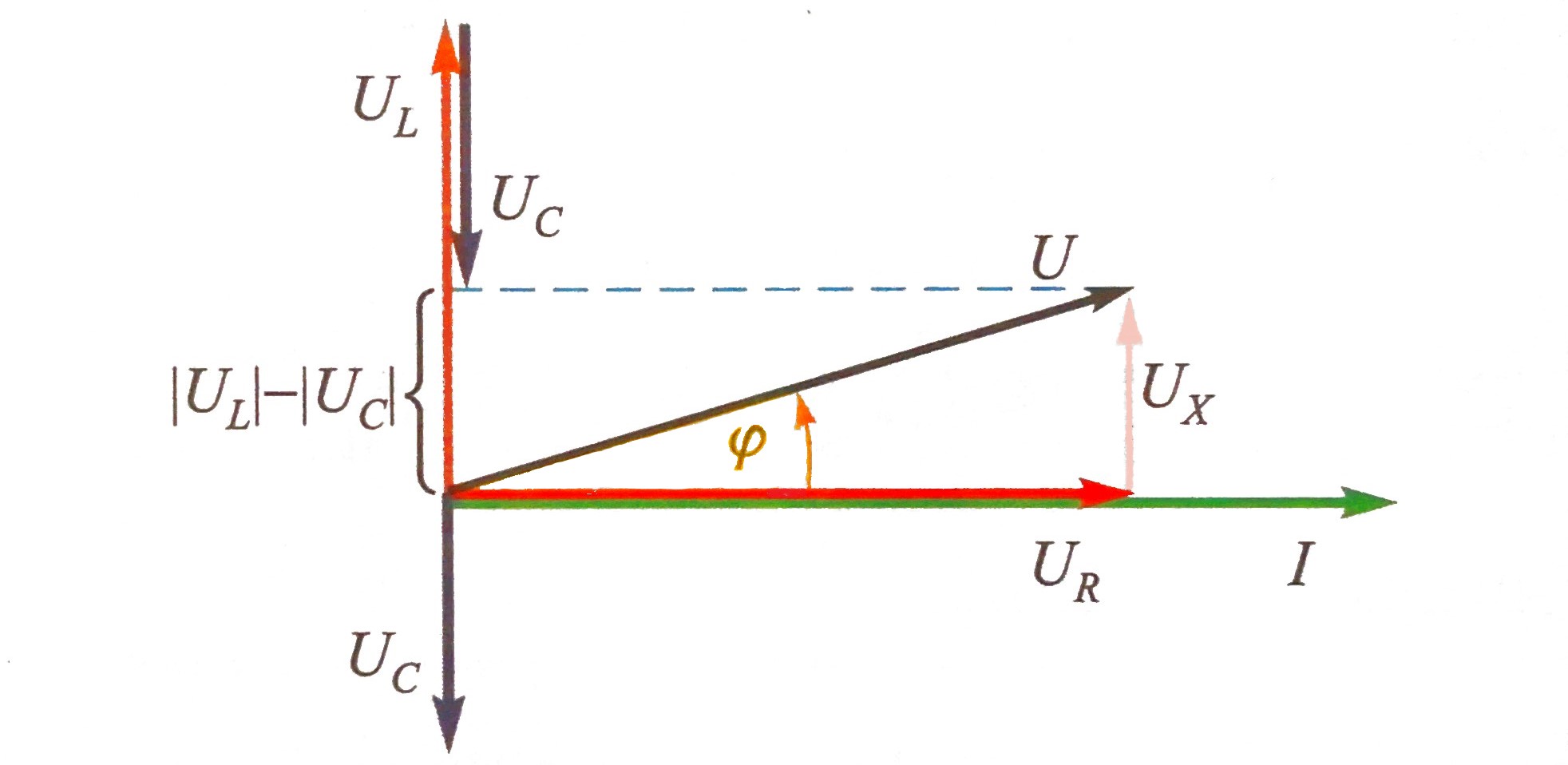
U vektorskom dijagramu (slika), vektor napon na otporu U_R u fazi je s vektorom struje I, koju uzimamo kao referentnu (s početnim kutem nula).

Napon na induktivitetu U_L prethodi struji za 90°, a napon na kapacitetu U_C istodobno zaostaje iza struje za 90°, pa je kut između ovih napona 180°.

U serijskom spoju, vektori napona na induktivitetu i kapacitetu suprotnog su smjera.

To znači da su ovi naponi u svakom trenutku suprotnih polariteta (kažemo da su naponi u protufazi).

Napon na serijskom spoju induktiviteta i kapaciteta iznosom je jednak razlici napona U_L i U_C, a ima smjer većeg od ovih napona. Kad je $U_L = U_C$, tad je napon na LC-spoju jednak nuli i sav napon izvora je na otporu R. U tom slučaju kažemo da je u serijskom RLC-krugu nastupila rezonancija.

Vektor ukupnog napona U jest vektorski zbroj napona na otporu, induktivitetu i kapacitetu.

U slučaju prikazanom na slici napon U_L veći je od napona U_C, pa ukupni napon U prethodi struji za kut φ. U slučaju kad je U_C veći od U_L tad ukupni napon zaostaje u fazi iza struje $ (φ \lt 0°) $. U rezonanciji napon U je u fazi sa strujom $ (φ = 0°) $. Iz trokuta napona na slici proizlazi jednadžba $$ U^2= U^2_R + (U_L - U_C)^2 $$ Dijeljenjem ove jednadžbe s I dobiva se izraz $$ (U / I)^2 = (U_R / I)^2 + (U_L / I - U_C / I)^2 $$ tj. $$ Z^2= R^2 + (X_L - X_C)^2 = R^2 + X^2 $$ Ova jednadžba opisuje trokut otpora (slika) gdje je ukupni reaktivni otpor X jednak razlici induktivnog i kapacitivnog otpora $ (X = X_L - X_C) $.

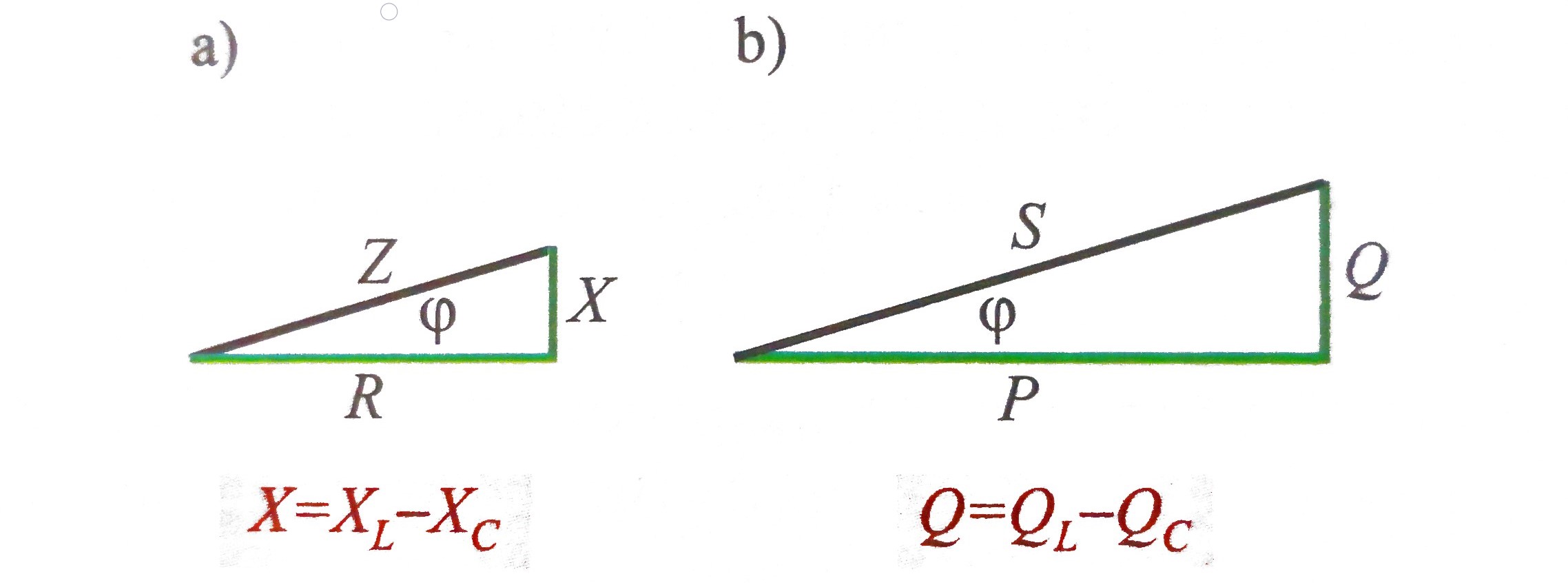
U rezonanciji je ukupni reaktivni otpor X jednak nuli pa je prividni otpor jednak radnom $ (Z=R) $.

U trokutu snage (slika) ukupna jalova snaga Q jednaka je razlici snage na induktivitetu i snage na kapacitetu $ (Q = Q_L - Q_C) $. Zbog suprotnih polariteta napona, induktivna i kapacitivna snaga suprotnih su predznaka. To znači da induktivitet daje energiju u trenutku kad ju kapacitet prima i obratno.

U rezonanciji ukupna jalova snaga je nula $ (Q=0) $, tj. kapacitivna ili induktivna snaga se poništavaju.

Paralelni RL-spoj

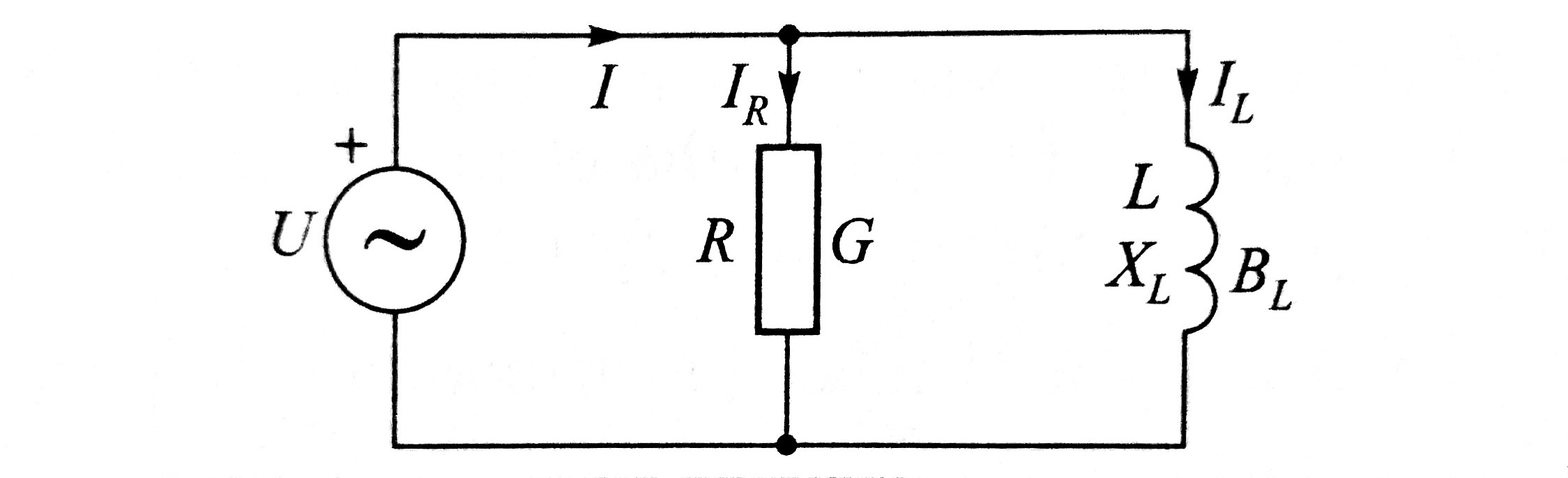
Kod paralelnog spoja otpora R i induktiviteta L (slika), napon je isti na oba elementa, a ukupna struja je zbroj struja pojedinih elemenata. Pri zbrajanju treba uzeti u obzir fazni pomak između struja. U tu svrhu se koristi njihov vektorski prikaz.

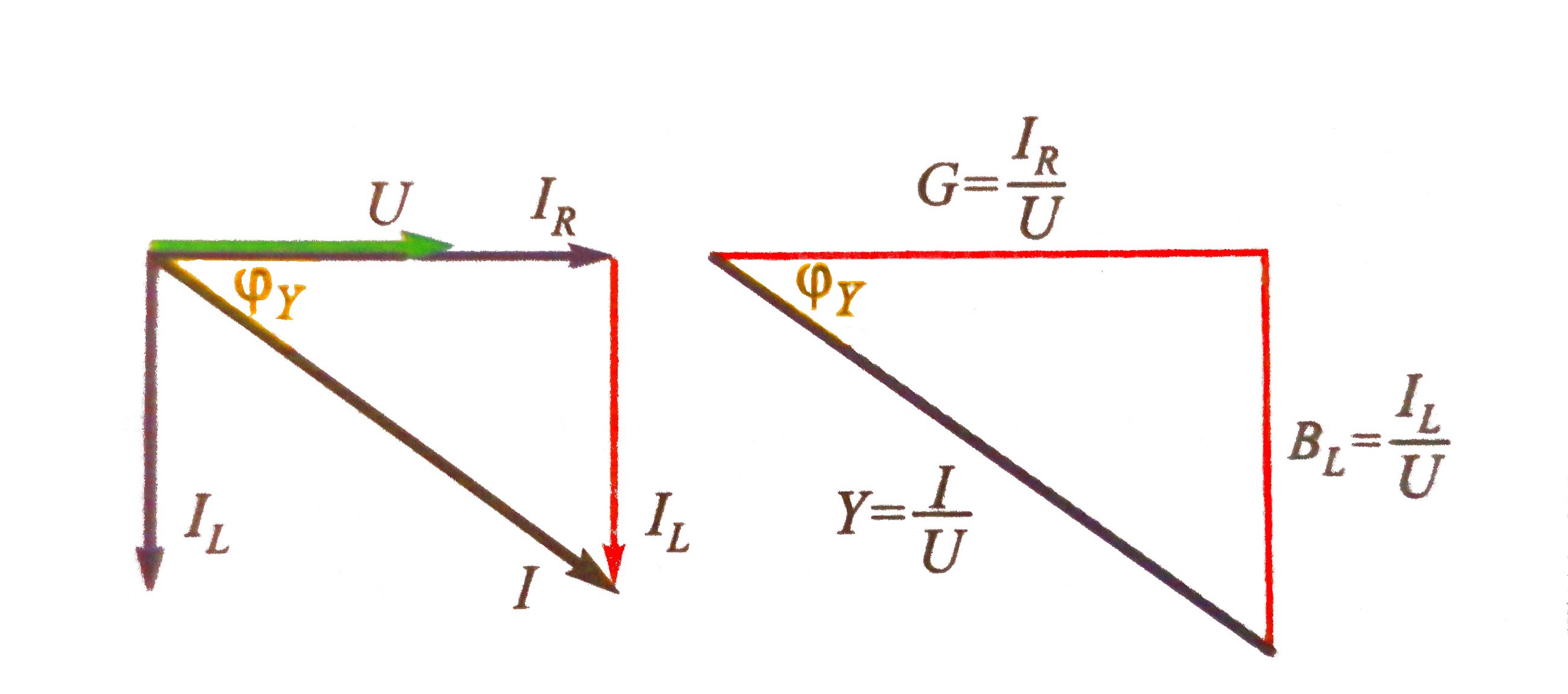
U vektorskom prikazu (slika) vektor napona U, (zajednički za oba elementa), uzimamo kao referentan i crtamo s kutem jednakim nuli.

Struja kroz otpor $I_R$ u fazi je s naponom, a struja kroz induktivitet $I_L$ zaostaje iza napona za 90°.

Vektor struje I je zbroj vektora struja $I_R$ i $I_L$. Ova tri vektora čine pravokutni trokut gdje je $$ I^2= I^2_R + I^2_L $$ Dijeljenjem stranica trokuta struja s naponom U da je sličan pravokutni trokut (slika), čije su katete jednake recipročnim vrijednostima radnog i induktivnog otpora, tj. vodljivostima elemenata.

Označavamo ih s $ G = I_R / U = 1 / R $ (radna vodljivost) i $ B_L = I_L / U = 1 / X_L = 1 / ωL $ (induktivna vodljivost), a taj trokut nazivamo trokut vodljivosti.

Hipotenuza ovog trokuta, jednaka je omjeru ukupne struje i napona $(I/U)$, ne predstavlja vdljivost nijednog elementa, pa se naziva prividna vodljivost (ili admitancija) i označava se s Y. Pritom vrijedi $$ Y^2= G^2 + B^2_L $$ Admitancija Y predstavlja vodljivost cijelog spoja i jednak je recipročnoj vrijednosti impendancije Z paralelnog RL-spoja $ (Y = 1/Z) $.

Kut ukupne struje I prema naponu U naziva se kut admitancije i označava s $φ_Y$. On je po iznosu jednak, a predznakom suprotan kutu impendancije $$ φ_Y=-φ $$ Ukupna struja I ovdje zaostaje iza napona, pa je kut admitancije negativan $ (-90° \lt φ_Y \lt 0°) $. To znači da je kut impendancije φ (tj. kut napona U prema struji I) pozitivan, što znači da napon U prethodi struji I (to je opće svojstvo induktivnog spoja).

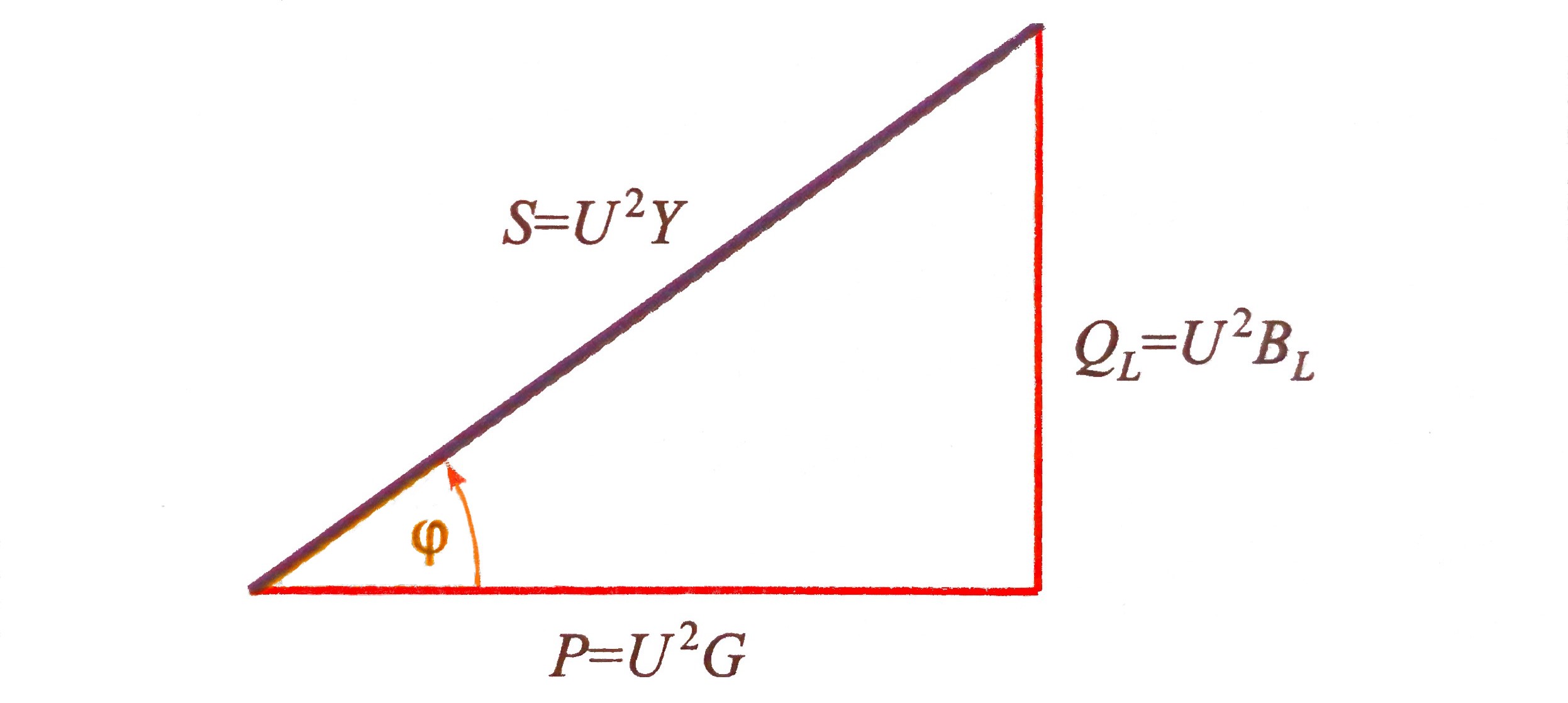
Snaga paralelnog RL-spoja računa se na slijedeći način:

Radna snaga $ P = I^2_R \cdot R = U^2 / R = U^2 \cdot G $
Jalova snaga $ Q_L = I^2_L \cdot X_L = U^2 / X_L = U^2 \cdot B_L $
Prividna snaga $ S = I^2 \cdot Z = U^2 / Z = U^2 \cdot Y $

Ova tri tipa snage čine trokut snage paralelnog RL-spoja prikazan na slici. Faktor snage je $P/S$.

Paralelni RC-spoj

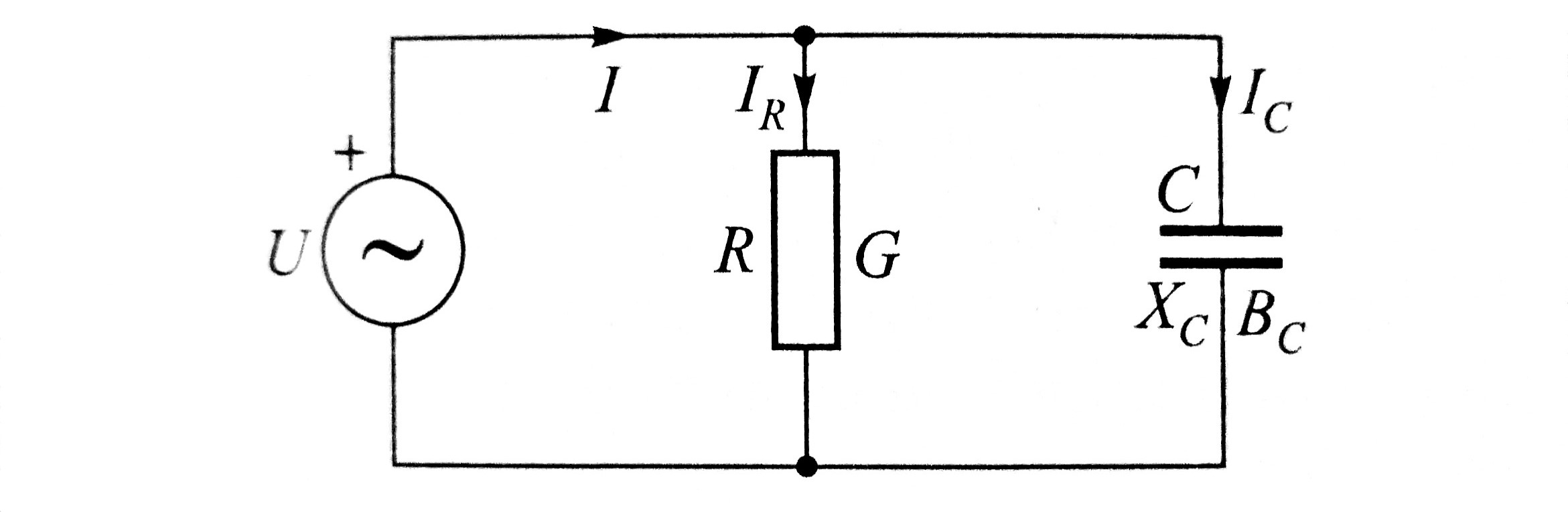
Kod paralelnog spoja otpora R i kapaciteta C (slika) napon U isti je na oba elementa. Slika prikazuje odnos vektora napona i struje.

Struja kroz otpor $I_R$ u fazi je s naponom U, a struja kroz kapacitet $I_C$ prethodi naponu za 90°.

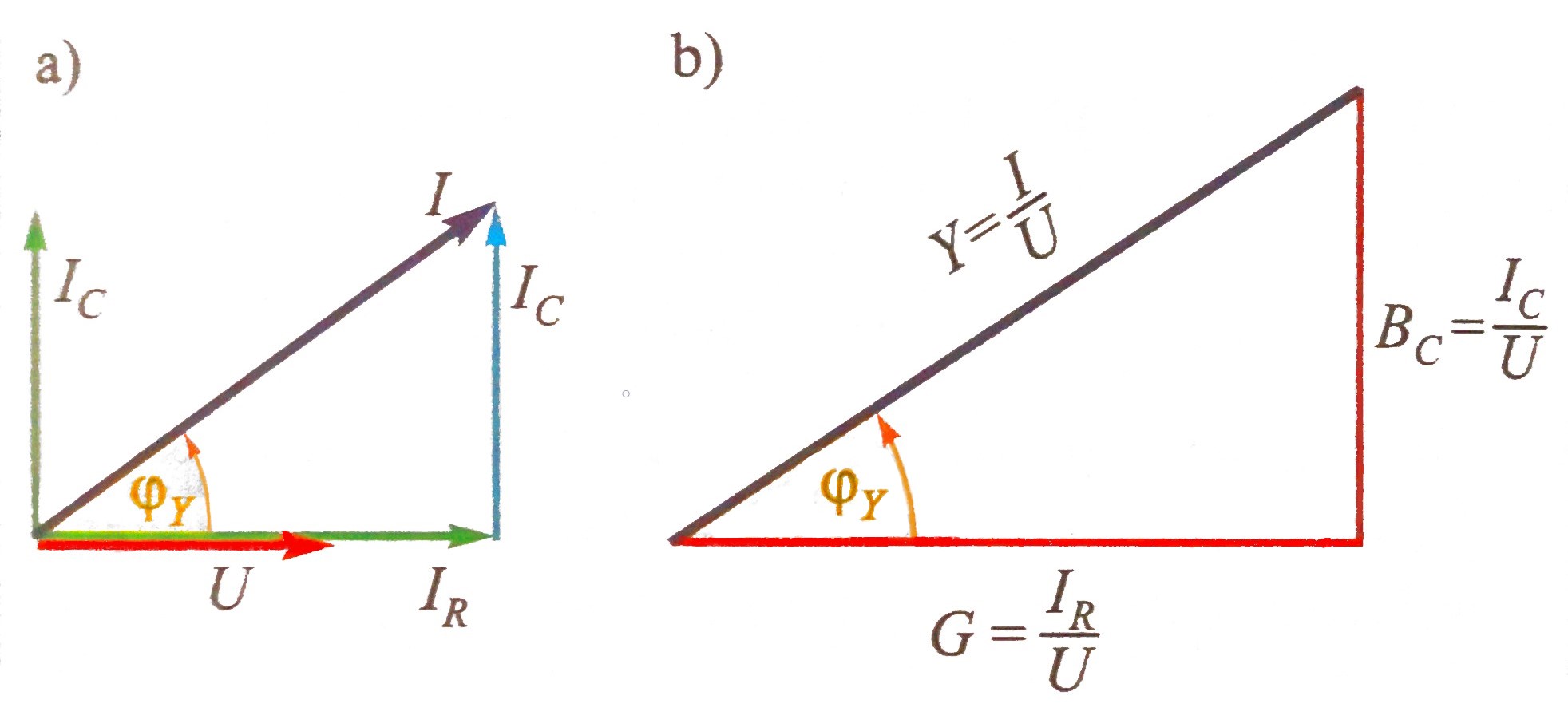
Vektor struje I je zbroj vektora struje $I_R \; i \; I_C$. Ova tri vektora čine pravokutni trokut gdje je $$ I^2=I^2_R + I^2_C $$ Dijeljenjem stranica trokuta struja s naponom U dobiva se sličan trokut nazvan trokut vodljivosti.

Katete ovog trokuta (slika) jednake su radnoj vodljivosti G $ (G=I_R/U=1/R) $ i kapacitivnoj vodljivosti B_C $ (B_C=I_L/U=1/X_C=ωC) $, a hipotenuza je jednaka prividnoj vodljivosti spoja Y, gdje je $$ Y^2=G^2 + B^2_C $$

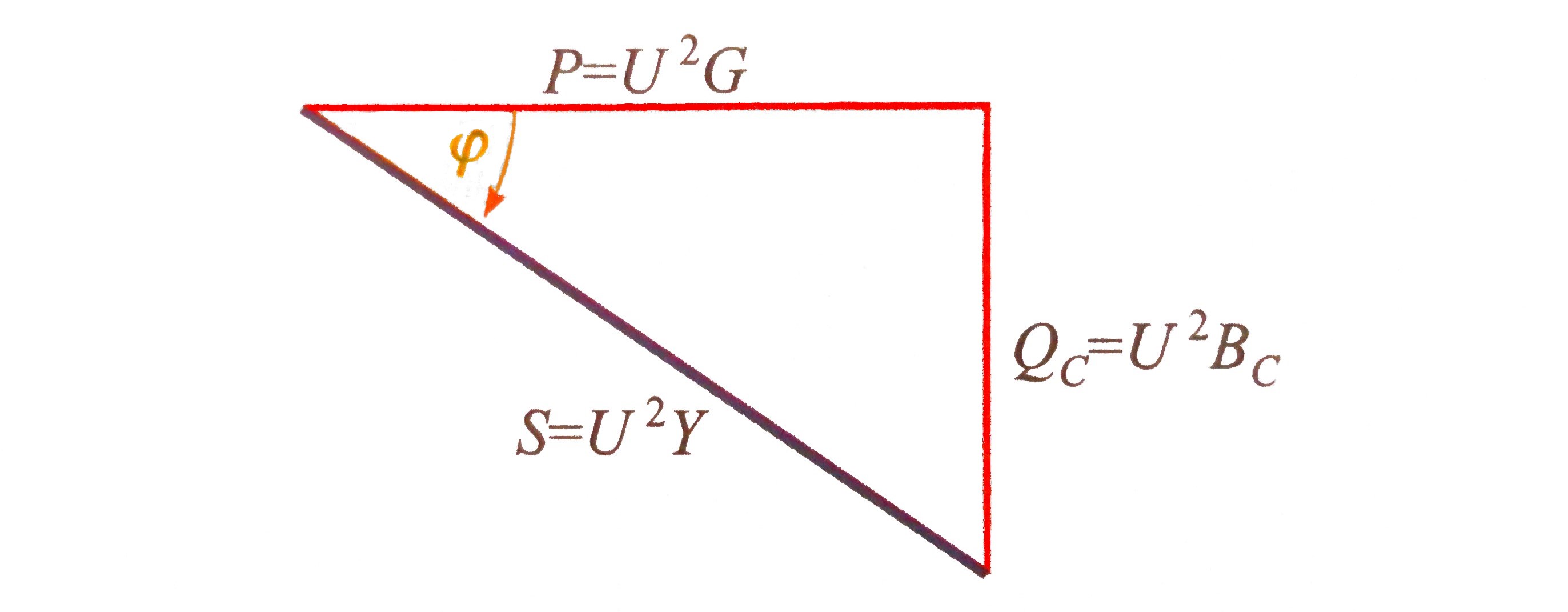
Ukupna struja I ovdje prethodi naponu U, pa je kut admitancije pozitivan $ (0° \lt φ_Y \lt 90°) $. To znači da je kut impendancije φ (tj. kut napona U prema struji I) negativan, što znači da napon zaostaje za strujom (to je opće svojstvo kapacitivnog spoja). Snaga paralelnog RC-spja računa se na slijedeći način:

Radna snaga $ P = I^2_R \cdot R = U^2 / R = U^2 \cdot G $
Jalova snaga $ Q_C = I^2_C \cdot X_C = U^2 / X_C = U^2 \cdot B_C $
Prividna snaga $ S = I^2 \cdot Z = U^2 / Z = U^2 \cdot Y $

Ova tri tipa snage čine trokut snage paralelnog RC-spoja prikazan na slici.

Iz trokuta sange proizlazi i faktor snage. On je, neovisno o spoju elemenata, uvijek jedank omjeru radne i prividne snage $ (P/S) $.

kad se zadaje faktor snage nekog trošila ili spoja, navodi se i njegov tip: induktivno ili kapacitivno.

Paralelni RLC-spoj

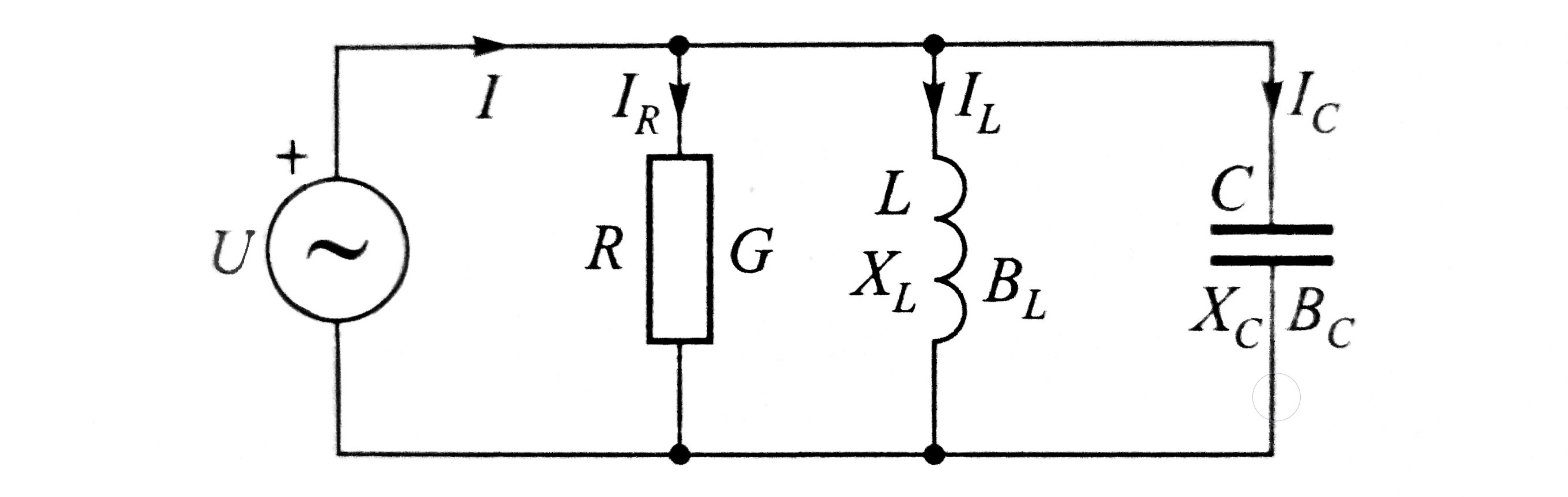
U paralelnom RLC-krugu (slika) uz radni otpor R paralelno su spojeni i oba tipa reaktivnih otpora, induktivni otpor $X_L$ i kapacitivi otpor $X_C$.

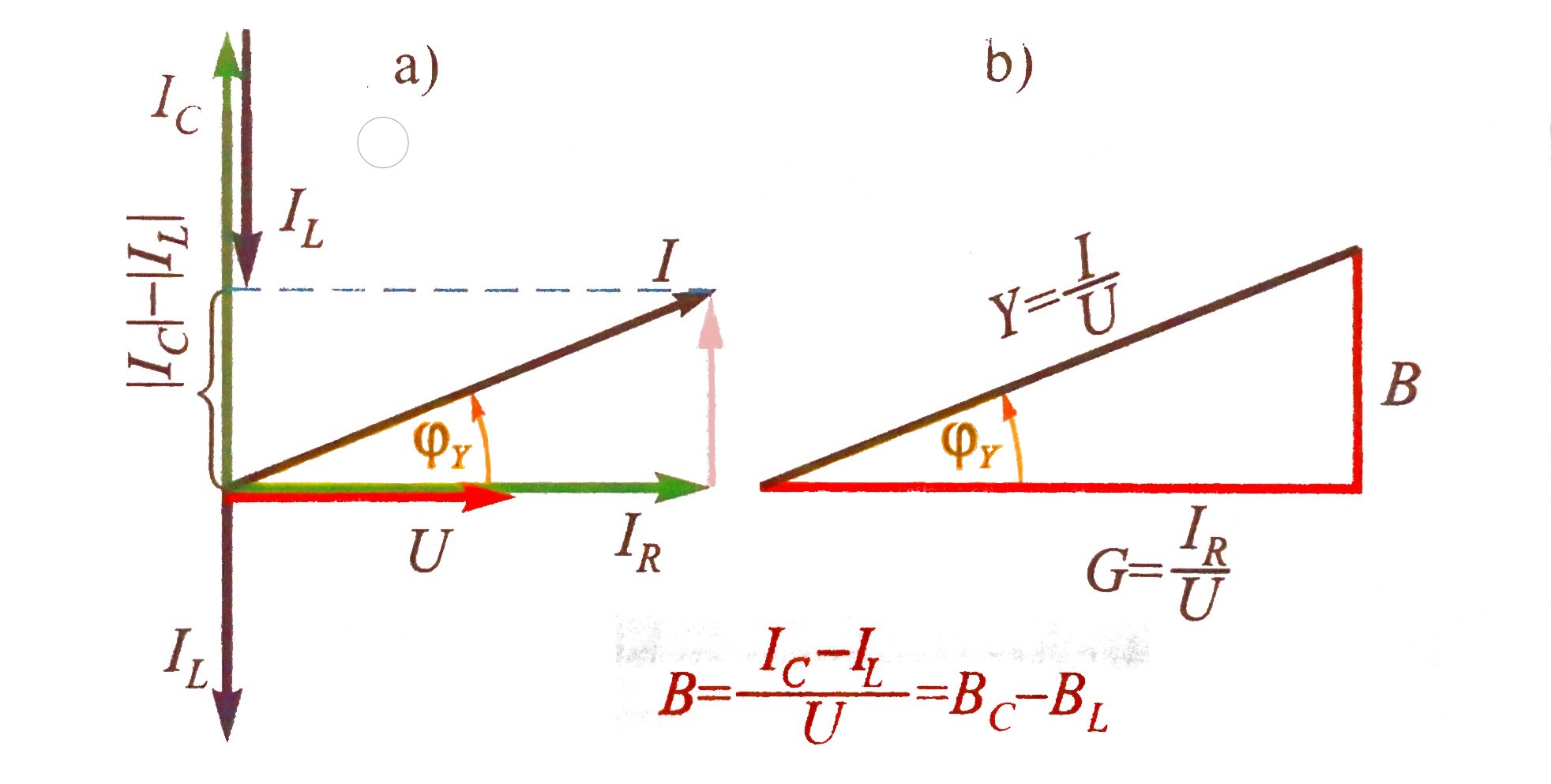
U vektorskom dijagramu (slika), vektori struje kroz otpor $I_R$ u fazi je s vektorom napona U, koji uzimamo kao referentan (s početnim kutem nula).

Struja kroz induktivitet $I_L$ prethodi naponu za 90°, dok struja kroz kapacitet $I_C$ zaostaje iza napona za 90°, pa je kut između ovih struja 180°.

U paralelnom spoju, vektori struja kroz induktivitet i kapacitet suprotnog su smjera.

To znači da su ove struje u svakom trenutku suprotnih smjerova (kažemo da su u protufazi).

Struja paralelnog spoja induktiviteta i kapaciteta iznosom je jednaka razlici struja $I_C \; i \; I_L$, a ima smjer veće od tih struja. Kad je $I_C=I_L$, tad je ukupna struja LC-spoja jednaka nuli i sva struja izvora teče kroz otpor R. Tada kažemo da je u paralelnom RLC-krugu nastupila rezonancija.

Vektor ukupne struje I jednak je vektorskom zbroju struja kroz otpor, induktivitet i kapacitet.

U slučaju prikazanom na slici struja $I_C$ veća je od struja $I_L$, pa ukupna struja I prethodi naponu U za kut $φ_Y$. U slučaju kad je $I_L$ veća od $I_C$ tad ukupna struja zaostaje u fazi iza napona $(φ_Y \lt 0)$.

Iznosi struja međusobno su povezani jednadžbom $$ I^2= I^2_R + (I_C - I_L)^2 $$ Dijeljenjem ove jednadžbe s U dobiva se izraz $$ (I / U)^2 = (I_R / U)^2 + (I_C / U - I_L / U)^2 $$ tj. $$ Y^2= G^2 + (B_C - B_L)^2 $$ Ovaj izraz opisuje trokut vodljivosti (slika). Ukupna reaktivna vodljivost B jednaka je razlici kapacitivne i induktivne vodljivosti $ (B=B_C-B_L) $.

Pri rezonanciji je ukupna reaktivna vodljivost $B=0$ (otpor paralelnog spoja L i C je beskonačan), pa je prividna vodljivost jednaka radnoj $(Y=G)$.

Zbog suprotnih smjerova struja $ I_L \; i \; I_C $, induktivna i kapacitivna snaga i tu su suprotnih predznaka.

To znači da induktivitet daje energiju u trenutku kad je kapacitet prima i obratno.

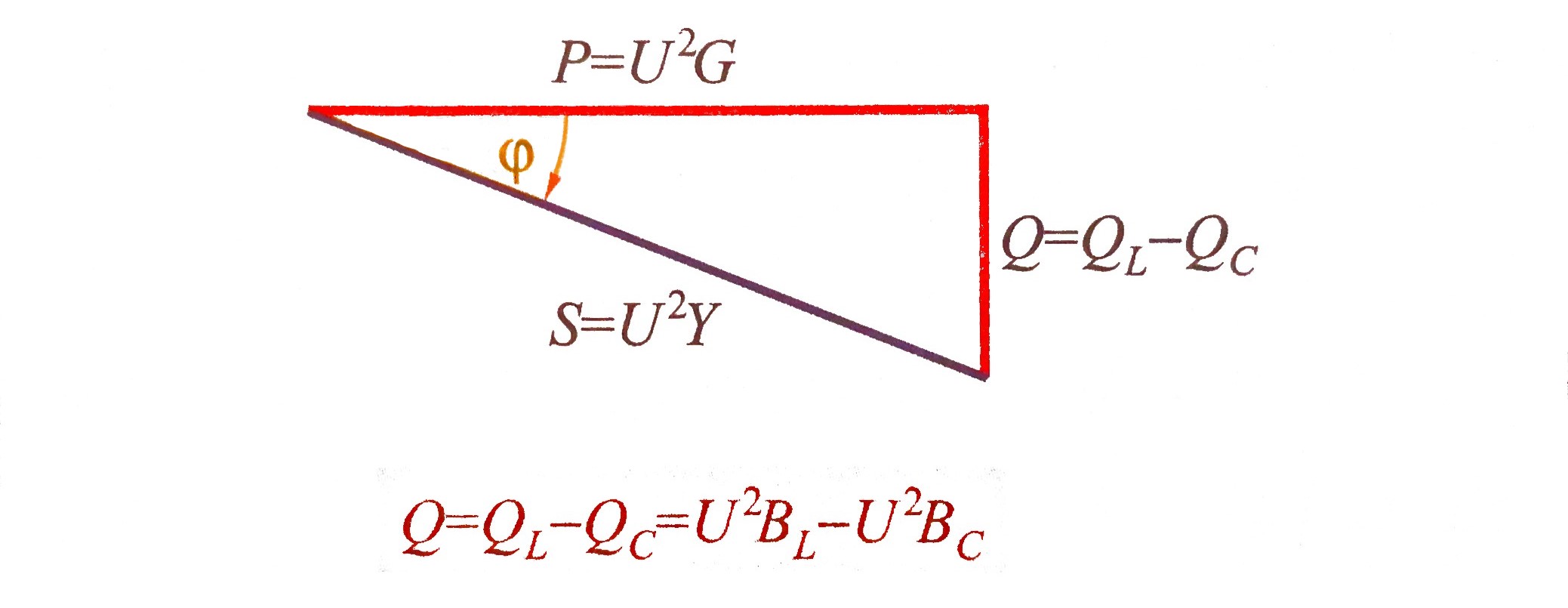
U trokutu snage (slika) ukupna jalova snaga Q jednaka je stoga razlici snage na induktivitetu i snage na kapacitetu $ (Q=Q_L-Q_C) $.

U rezonanciji ukupna jalova snaga $(Q=0)$, tj. snage na kapacitetu i induktivitetu se kompenziraju.