KONDENZATORI

Pojam električnog kapaciteta

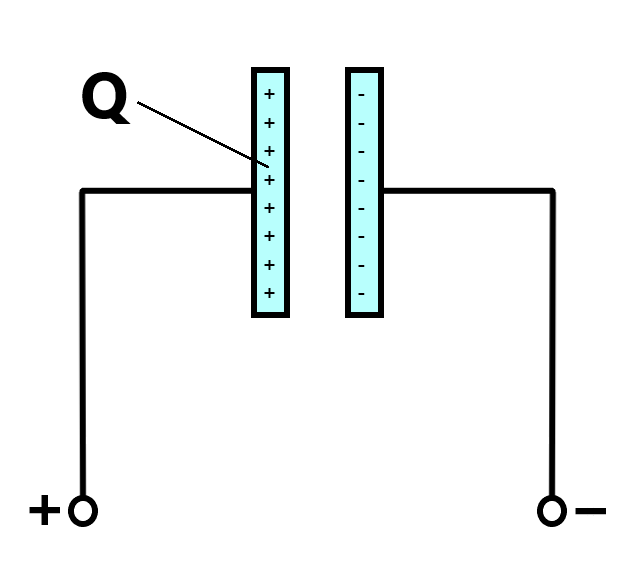Priključimo li međusobno izolirane pločaste elektrode na izvor, na njima će se pod utjecajem napona izvora razdvojiti jednake količine naboja suprotnog predznaka, koji će u izolatoru među pločama stvoriti električno polje.

Odspojimo li potom elektrode izvora, razdvojeni naboj ostat će i dalje na pločama vezani međusobno električnom silom, a odvojeni dielektrikom u kojem stvaraju električno polje.

Na taj način, u ovom sustavu vodljivih elektroda razdvojenih izolatorom, može se pohraniti električni naboj. Količina pohranjenoog naboja Q pritom je razmjerna naponu U između elektroda.
\[Q \sim U \]
To znači da je za određeni sustav elektroda (i vrstu izolatora) stalan omjer između pohranjenog naboja Q i napona U među elektrodama. Taj omjer naziva se električni kapacitet sustava. Oznaka kapaciteta je C, a jedinica je farad (F)
\[C = {Q \over U} \qquad [C]={As \over V} = F\] Sustav vodljivih tijela ima kapacitet od 1 F, ako uz napon od 1 V može pohraniti naboj od 1 As.

U stvarnosti su kapaciteti mnogistruko manji od 1 F, do reda veličine nF (10^-9F) i pF (10^-12F).

Između bilo koja dva, međusobno izolirana, vodljiva tijela postoji neki kapacitet.

Kapacitet u krugu izmjenične struje

Dovede li se na kondenzator kapaciteta C izmjenični napon, zbog stalne promjene polariteta napona, kondenzator se naizmjenično nabija i izbija.

Kako naboji pritom struje naizmjenično na ploče kondenzatora i s njih, kroz kapacitet kao da teče izmjenična struja.

Kapacitivni otpor

Uz sinusoidni napon, u krugu s kapacitetom C i struja je sinusoidnog oblika i jednake frekvencije.

Amplituda (vršna vrijednost) struje I_m pritom je razmjerna amplitudi napona U_m, kružnoj frekvenciji ω i kapacitetu kondenzatora C, tako da je \[I_m = ω \cdot C \cdot U\] Omjer amplituda napona i struje ovdje određuje otpor koji kapacitet predstavlja izmjeničnoj struji. Taj se otpor naziva kapacitivni otpor i označava s X_C. \[{U_m \over I_m} = {U \over I} = {1 \over ω \cdot C} = X_C\]

Kapacitivna jalova snaga

Umnožak struje i napona na kapacitetu daje sinusoidu trenutačne snage čija je srednja vrijednost, tj. radna snaga jednaka nuli (slika).

Umnožak efektivnih vrijednosti struje i napona, tj. snaga na kapacitetu stoga se (za razliku od radne snage) naziva jalova snaga i označava s \(Q_C\). $$ Q_C = U \cdot I = \frac{U^2}{X_C} = I^2 \cdot X_C $$

Serijski spoj

Spoj dvaju kondenzatora u kojem naboj iz izvora može doći samo na vanjske ploče spoja, dok su unutarnje ploče od izvora odvojene izolatorom. Kako se međutim unutarnje ploče nalaze u polju nabijenih vanjskih ploča, na njima se influencijom razdvaja naboj i to upravo tolikog iznosa koliki je naboj vanjskih ploča.
Rezultat toga je da su oba kondenzatora nabijena i to jednakim količinama naboja. Međusobno jednaki naboji Q₁ i Q₂ ovako spojenih kondenzatora jednaki su ujedno i ukupnom naboju Q koji je izvor razdvojio na cijelom spoju, tj. \[{Q_1}={Q_2}={Q}\]
Ovakav spoj gdje je ukupni naboj spoja jednak naboju svakog pojedinog kondenzatora naziva se serijski spoj kondenzatora.

Prema Kirchhoffovom zakonu za napone, u serijskom spoju ukupni napon na spoju U_uk jednak je zbroju napona pojedinih kondenzatora, U₁ i U₂ \[{U_{uk}}={U_1}+{U_2}\] Uvrste li se ovi naponi izraženi pomoću naboja i kapaciteta (gdje je C_uk ukupni kapacitet spoja) \[U_{uk} = {Q \over C_{uk}} \qquad U_1 = {Q \over C_1} \qquad U_2 = {Q \over C_2}\] dobiva se sljedeća jednadžba \[{Q \over C_{uk}} = {Q \over C_1} + {Q \over C_2} \] koja (djeljenjem s Q) daje izraz za ukupni kapacitet C_uk serijskog soja dvaju kondenzatora \[{1 \over C_{uk}} = {1 \over C_1} + {1 \over C_2} \quad tj. \quad C_{uk} = {{C_1 \cdot C_2} \over {C_1 + C_2}} \] Općenito za serijski spoj n kondenzatora vrijedi \[{1 \over C_{uk}} = {1 \over C_1} + {1 \over C_2} + ... + {1 \over C_n} \] U serijskom spoju, recipročna vrijednost ukupnog kapaciteta jednaka je zbroju recipročnih vrijednosti pojedinih kapaciteta.

Na serijski spojenim kondenzatorima napon se dijeli obrnuto razmjerno njihovim kapacitetima $${{U_1 \over U_2} = {C_2 \over C_1}}$$ Za serijski spoj kondenzatora kaže se da je kapacitivno djelilo napona.

• content_pastePrimjer 1
  Ako su kapaciteti kondenzatora C₁ = 3 pF i C₂ = 6 pF, a ukupni napon U = 24 V, odredite ukupni kapacitet C_uk i ukupni naboj Q_uk spoja, te naboje (Q₁ i Q₂) i napone (U₁ i U₂) na kondenzatorima. $${C_{uk} = {{C_1 \cdot C_2} \over {C_1 + C_2}} = {{3 \cdot 6} \over {3 + 6}} \ pF = {18 \over 9} \ pF = 2 \ pF}$$ $${Q_{uk} = {C_{uk} \cdot U} = {{2 \cdot 10^{-12} F } \cdot {24 \ V}} = {48 \cdot 10^{-12} As } = {48 \ pAs}}$$ $${Q_1 = Q_2 = Q_{uk} = 48 \ pAs}$$ $${U_1 = {Q_1 \over C_1} = {48 \ pAs \over 3 \ pF} = {16 \ V}}$$ $${U_2 = {Q_2 \over C_2} = {48 \ pAs \over 6 \ pF} = {8 \ V}}$$

Paralelni spoj

Kondenzatori na slici spojeni su tako da imaju isti napon, koji je jednak ukupnom naponu spoja \[{U_1}={U_2}={U}\]

Naboj je ovdje razdijeljen na pojedine kondenzatore (pozitivni na gornjim, a negativni na donjim pločama), tako da je ukupni naboj spoja jednak zbroju naboja pojedinih kondenzatora, tj. \[Q={Q_1}+{Q_2}\] Dijeljenjem ove jednadžbe naponom U dobivamo \[{Q_{uk} \over U}={Q_1 \over U}+{Q_2 \over U}\] Omjer ukupnog naboja Q_uk i ukupnog napona U spoja određuje ukupni kapacitet spoja C_uk, pa uz \[C_{uk} = {Q_{uk} \over U} \qquad C_1 = {C_1 \over U} \qquad C_2 = {C_2 \over U}\] dobivamo izraz za ukupni kapacitet ovoga spoja \[{C_{uk}}={C_1}+{C_2}\] Općenito, za paralelni spoj n kondenzatora vrijedi \[{C_{uk}}={C_1}+{C_2}+...+C_n\] Na paralelno spojenim kondenzatorima naboj se dijeli razmjerno njihovim kapacitetima $${{Q_1 \over Q_2} = {C_1 \over C_2}}$$

• content_pastePrimjer 2
  Koliki najveći, a koliki najmanji kapacitet se može postići spajanjem n= 10 jednakih kondenzatora pojedinačnog kapaciteta C= 10 pF
  Paralelnim spajanjem n kondenzatora kapaciteta C postiže se n puta veći ukupni kapacitet: $$ C_{max} = {n \cdot C} = 100 \ pF $$ Serijskim spajanjem n kondenzatora kapaciteta C postiže se n puta manji ukupni kapacitet: $$ C_{min} = {C \over n} = 1 \ pF $$
• content_pastePrimjer 3
  U paralelnom spoju kondenzatora uz napon U= 100 V ukupni naboj je Q_uk= 3,2 mAs. Ako je kapacitet kondenzatora C₁= 10 µF odredite kapacitet kondenzatora C₂, te naboje na pojedinim kondenzatorima (C₁ i C₂). $$ {C_{uk} = {Q_{uk} \over U} = {{3,2 \cdot 10^{-3} \ As} \over {100 \ V}} = {32 \cdot 10^{-6} \ F } = {32 \ µF}} $$ \[C_{uk} = {C_1 + C_2} \qquad C_2 = {C_{uk} - C_1} = {32 \ µF - 10 \ µF} = {22 \ µF} \] \[Q_1 = {C_1 \cdot U} = {(10 \cdot 10^{-6} \ F) \cdot 100 \ V} = 10^{-3} \ As = 1 \ mAs \] \[Q_2 = {C_2 \cdot U} = {(22 \cdot 10^{-6} \ F) \cdot 100 \ V} = 2,2 \cdot 10^{-3} \ As = 2,2 \ mAs \]