Ohmski otpor

Električni otpor

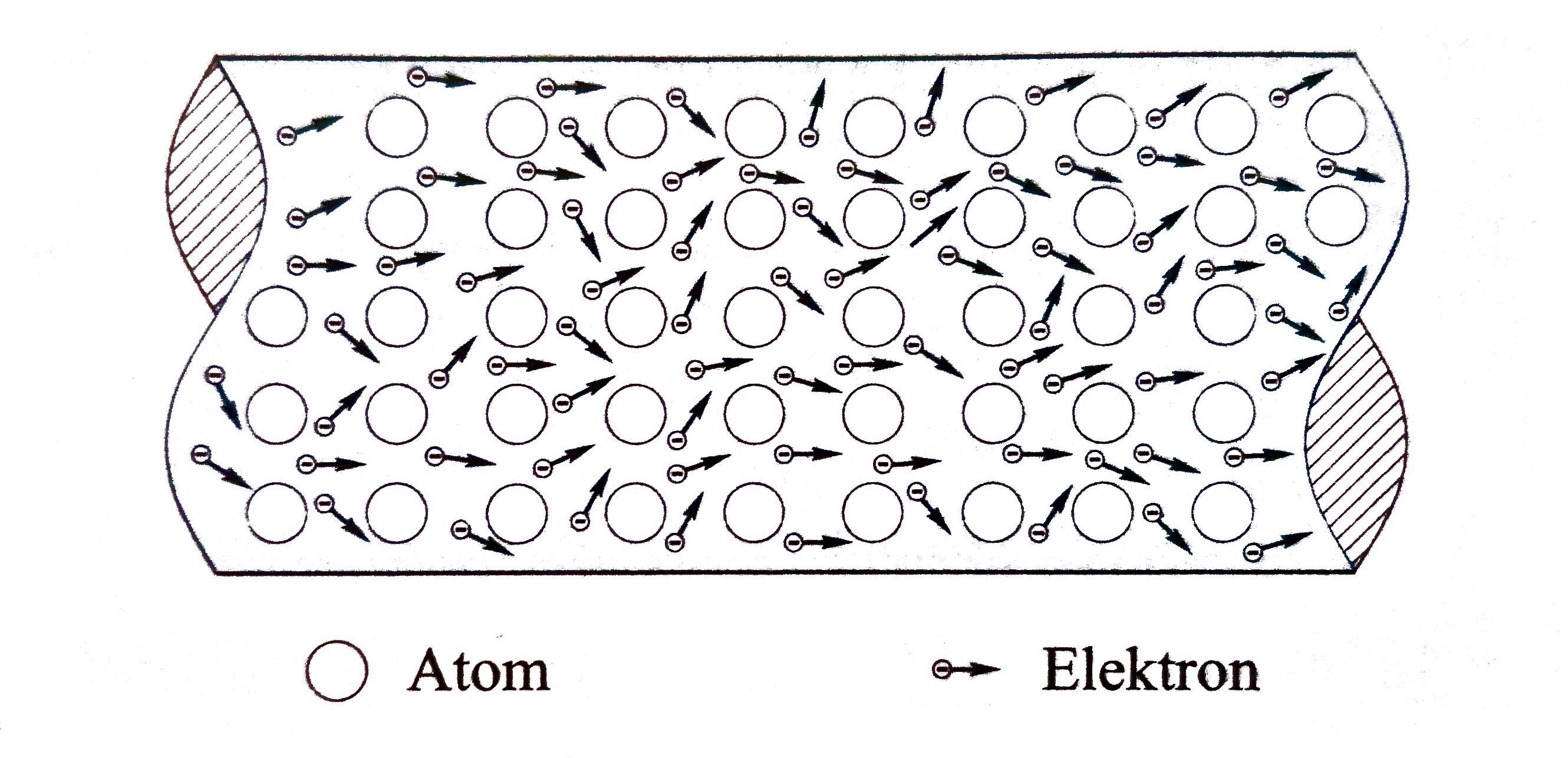
Pri toku struje kroz metalnu žicu (vodič) slobodni elektroni nailaze na atome koji (zbog topline) titraju oko svojih ravnotežnih položaja u kristalnoj rešetki materijala. Možemo zamisliti da atomi tako priječe slobodni put elektronima, što se očituje kao opiranje tvari protoku električne struje.

Ovim otporom ograničena je jakost struje, a za njegovo razumijevanje zgodna je zamisao sudara elektrona s atomima u metalu.

Elektroni sudarom gube dio energije, pa za održavanje struje (zbog otpora) treba trošiti rad. Atom sudarom dobiva energiju, čime se pojačava njegovo titranje, a to znači povećanje temperature.

Ne samo kod struje elektrona u krutini, nego i kod struje iona u vodljivoj tekućini javlja se otpor na čije svladavanje naboji troše rad. Otporno djelovanje javlja se čak i kod struje u vodljivom plinu.

Općenito, naboji pri strujanju nailaze na otporna djelovanja za svladavanje kojih troše rad. Ta otporna djelovanja nazivaju se električni radni otpor (kraće električni otpor, ili samo otpor).

Oznaka za električni otpor je R, a jedinica je om. Oznaka za om je Ω (grčko slovo omega). $$ [R] = Ω $$

Otpor vodiča

Otpor vodiča razmjeran je duljini vodiča l, a obrnuto razmjeran njegovom presjeku S.

Faktor razmjernosti različit je za pojedini materijal te predstavlja svojstvo tvari koja se naziva otpornost (ili specifični otpor) i označava s ρ (grčko slovo ro).

Na temelju toga, otpor vodiča računa se kao $$ R = ρ {l \over S} $$ Ova jednadžba pokazuje da će npr. dvaput dulja žica (istog presjeka i materijala) imati dvaput veći el. otpor, dok će žica dvaput većeg presjeka (iste duljine i materijala) imati upola manji otpor.

Električna vodljivost

El. vodljivost je recipročna vrijednost otpora.

Oznaka vodljivosti je G, a jedinica je simens (S) $$ G = {1 \over R} \qquad [G]={1 \over Ω}=S $$ Vodljivost je kao i otpor, svojstvo fizičkog tijela. Obrnuto od otpora, koji pokazuje koliko se tijelo opire protjecanju struje, vodljivost pokazuje kolikon dobro tijelo vodi struju.

Ohmov zakon

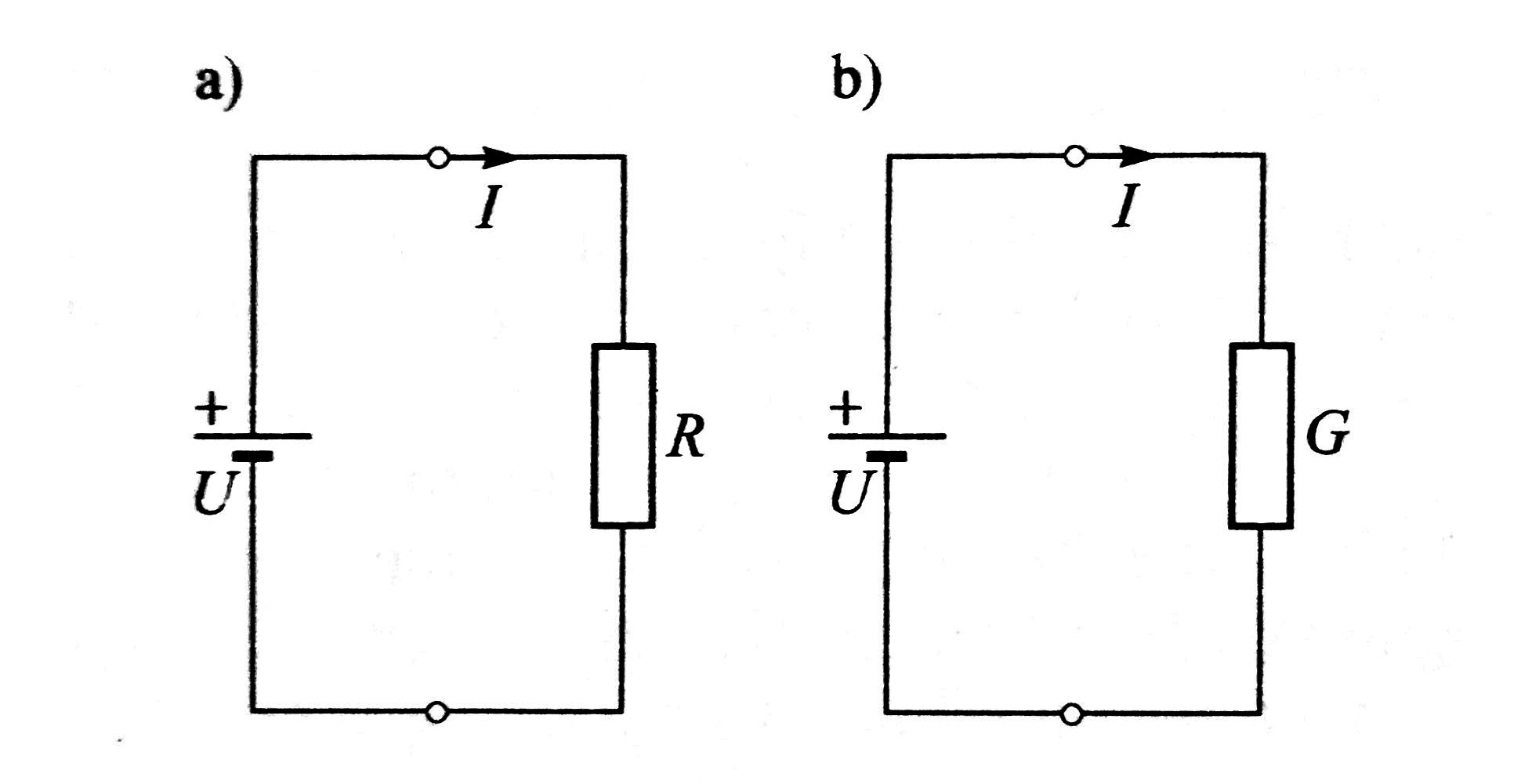
Uočeno je da jakost struje u krugu ovisi samo o naponu i otporu kruga. Pokazuje se da jakost struje I raste s naponom U, a opada s porastom otpora R. Napiše li se to u obliku jednadžbe, dobiva se jedan od temeljnih zakona elektrotehnike, poznat kao Ohmov zakon: $$ I = {U \over R} $$ Ohmov zakon može se općenito iskazati ovako:

Ohmov zakon može se napisati u tri oblika: $$ {I = {U \over R}} \qquad {U = I \cdot R} \qquad {R = {U \over I}} $$ koji se mogu izraziti na sljedeće načine:

• - izvor daje struju jakosti I koja je jednaka omjeru napona izvora U i otpora kruga R; ili
• - napon U na otporniku jednak je umnošku otpora R i jakosti struje I otpornika; ili
• - otpor otpornika R jednak je omjeru napona na otporniku U i jakosti struje kroz otpornik I.

Iz zadnje jednadžbe proizlazi i definicija jedinice električnog otpora, tj. 1 V kroz 1 A daje 1 Ω: $$ [R]={V \over A}=Ω $$ Umjesto otpora u Ohmov zakon može se uvesti i njegova recipročna vrijednost tj. vodljivost G (G=1/R), pa se dobiju sljedeći izrazi: $$ {I = G \cdot U} \qquad {U = {I \over G}} \qquad {G = {I \over U}} $$ iz čega proizlazi i definicija za jedinicu el. vodljivosti (simens), tj. 1 A kroz 1 V daje 1 S: $$ [G]={A \over V}=S={1 \over Ω} $$

Serijski spoj otpora

U krugu gdje struja teče kroz otpornike koji su spojeni u nizu, takav spoj elemenata nazivamo serijski.

U krugu na slici na izvor napona U serijski su spojeni otpori R₁, R₂ i R₃.
Na njima su naponi: $$ {U_1=I \cdot R_1} \qquad {U_2=I \cdot R_2} \qquad {U_3=I \cdot R_3}$$ Označimo li s R_uk ukupni otpor serijskog spoja otpora R₁, R₂ i R₃ (slika), napon izvora možemo izraziti kao $$ U = I \cdot R_{uk} $$ Uvrstimo li jednadžbu Kirchhoffovog zakona $$ U = U_1 + U_2 + U_3 $$ napone izražene pomoću struje i otpora dobivamo $$ I \cdot R_{uk} = I \cdot R_1 + I \cdot R_2 + I \cdot R_3 = I \cdot (R_1 + R_2 + R_3) $$ i konačno, dijeljenjem cijele jednadžbe s I dobiva se izraz za ukupni otpor serijskog spoja $$ R_{uk} = R_1 + R_2 + R_3 $$ Općenito, za serijski spoj n otpora ukupni otpor jednak je zbroju svih otpora spojenih u seriju. $$ R_{uk} = R_1 + R_2 + R_3 + ... + R_n $$

Paralelni spoj otpora

Za paralelni spoj otpora na slici vrijedi jednadžba Kirchhoffovog zakona za struje $$ I = I_1 + I_2 + I_3 $$ Dijeljenjem obje strane jednadžbe s naponom izvra dobiva se sljedeći izraz $$ {I \over U} = {I_1 \over U} + {I_2 \over U} + {I_3 \over U} $$ Posjetimo se da je omjer struje i napona jednak recipročnoj vrijednosti otpora ili el. vodljivosti G.

Na desnoj strani jednadžbe su vodljivosti pojedinih paralelnih grana, dok lijeva strana (omjer struje i napona izvora) predstavlja ukupnu vodljivost kurga, što se može napisati kao $$ G_{uk} = G_1 + G_2 + G_3 $$

Općenito za ukupni otpor R_uk paralelnog spoja n otpora R₁, R₂ do R_n vrijedi sljedeća jednadžba $$ {1 \over R_{uk}} = {1 \over R_1} + {1 \over R_2} + ... + {1 \over R_n} $$ Otpor i vodljivosti opisuju isto svojstvo elemenata električnog kurga. Dok je analiza serijskog spoja jednostavnija pomoću otpora, pojam vodljivosti olakšava analizu i proračun paralelnog spoja.

Za neke slučajeve paralelnog spoja izvedene su gotove jednadžbe za izračun ukupnog otpora:

Ukupni otpor dvaju paralelno spojenih otpora R₁ i R₂ (slika) računa se na temelju toga kao: $$ R_{uk}={{R_1 \cdot R_2} \over {R_1 + R_2}} $$

Složeni spojevi otpora

Ma koliko složeni, spojevi otpora u el. krugovima mogu se uvijek predstaviti kombinacijom jednostavnih (serijskih i paralelnih) spojeva opisanih u predhodnim poglavljima.

Već smo vidjeli kako se određuje ukupni otpor serijskog ili paralelnog spoja otpora. Ukupni otpor predstavlja omjer ukupnog napona i ukupne struje spoja, i njime se prema van može nadomjestiti serijski ili paralelni spoj otpora.

Općenito, bilo kako složeni spoj otpora između dviju točaka el. kruga može se nadomjestiti jednim otporom. Taj otpor, koji je jednak omjeru napona i struje između prmatranih točaka kruga, nazivamo nadomjesni (ili ekvivalentni) otpor.

Na primjeru složenog spoja otpora sa slike pokazat ćemo postupak određivanja nadomjesnog otpora. Na slici , otpori R₁ i R₂ spojeni su serijski, a njima paralelno spojen je otpor R₃.

Prvi korak jest odrediti otpor serijskog spoja R₁ i R₂ (označimo ga kao R_1-2): $$ R_{1-2}=R_1 + R_2 $$ Spoj sa slike možemo pojednostavljeno prikazati kao paralelni spoj otpora R_1-2 i otpora R₃ (slika). Sljedeći korak (i završni) jest odrediti otpor paralelnog spoja (označimo ga s R_1-2-3): $$ R_{1-2-3} = {{ R_{1-2} \cdot R_3 } \over { R_{1-2} + R_3 }} = R_{nad} $$ a to je i nadomjesni otpor cijelog spoja (slika)

Poznavajući napon na složenom spoju otpora, pomoću nadomjesnog otpora možemo odrediti ukupnu struju spoja. Potom je lako (pomoću Kirchhoffovih zakona) odrediti raspodjelu struja i napona na pojedninm otporima složenog spoja.

Otpor u krugu izmjenične struje

Struja i napon na otporu

Na otporu su napon u_t i struja i_t povezani u svakom trenutku Ohmovim zakonom preko otpora R: $$ u(t) = R \cdot i(t) = R \cdot I_m \sin(\omega t) = U_m \sin(\omega t) $$ To znači da sinusoida napona na otporu ima nule i maksimume istodobno kad i sinusoida struje, tj. između struje i napona nema faznog pomaka. Kažemo da su na otporu napon i struja u fazi.

Na slici su vektori i vremenski prikazi struje i napona na otporu. Omjer vršnih (i efektivnih) vrijednosti napona i struje jednak je otporu R $$ \frac{U_m}{I_m} = \frac{U}{I} = R $$

Snaga na otporu

Snaga na nekom elementu električnog kruga, prisjetimo se, jednaka je umnošku napona i struje $$ p(t) = u(t) \cdot i(t) $$ Na slici prikazane su vremenske funkcije struje, napona i trenutačne snage na otporu p_t . Trenutačna snaga, kao umnožak sinusoida napona i struje, također je sinusoida, ali dvostruke frekvencije.

Snaga na otporu vremenski se mijenja po sinusoidi koja je cijela pomaknuta u pozitivno područje.

Pozitivni predznak snage znači da otpor stalno prima energiju. Ova snaga određuje energiju koja se nepovratno pretvara u toplinu (električni rad), pa se naziva radna (djelatna) snaga (oznaka P).

Srednja vrijednost snage (snaga na otporu) je sredina između najmanje (0) i najveće snage \((U_m I_m)\). $$ P = \frac{U_m \cdot I_m}{2} = \frac{U_m}{\sqrt 2} \cdot \frac{I_m}{\sqrt 2} = U \cdot I = \frac{U^2}{R} = I^2 \cdot R $$